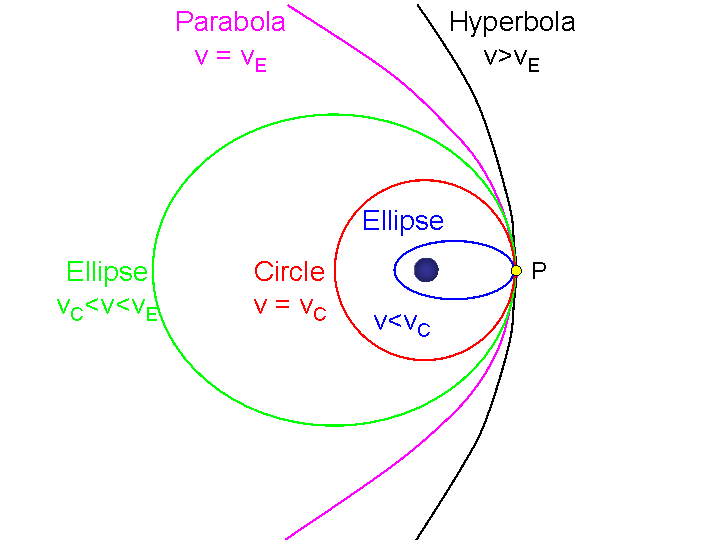
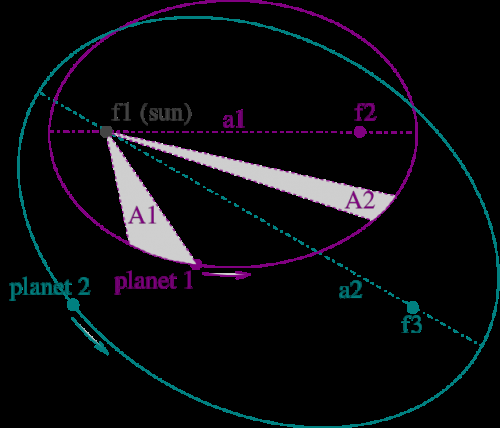
A Satellite Is In A Circular Orbit About The Earth At A Distance Of One Earth Radius

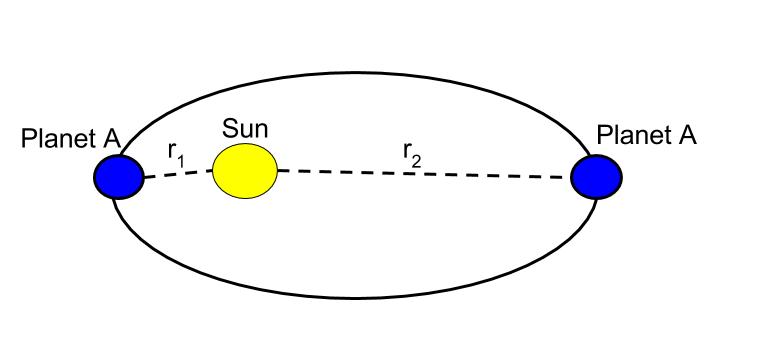
A satellite circles the earth in an orbit whose radius is twice the earth s radius as measured from the center of the earth.

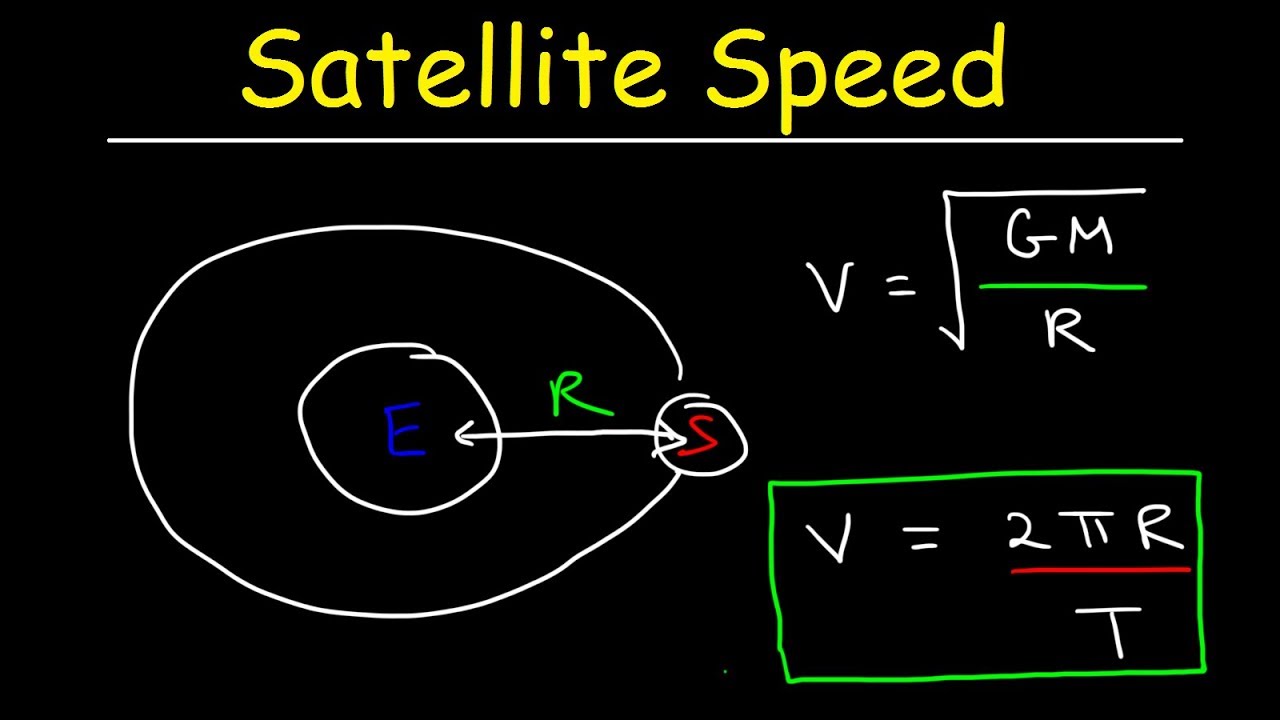
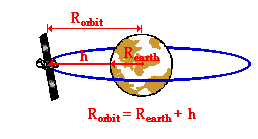
A satellite is in a circular orbit about the earth at a distance of one earth radius. 6 371 times 10 to the sixth meters. If you just multiply this by 1 000. You have to use the distance from the center of the earth not the distance above earth s surface as the radius. Units m s b find the period of its revolution.

A satellite is in a circular orbit about the earth at a distance of one earth radius above the surface. What is the velocity of the satellite. A 718 kg satellite is in a circular orbit about the earth at a height above the earth equal to the earth s mean radius a find the satellite s orbital speed. Therefore the distance you use in the equation is the distance between the two orbiting bodies.

A find the satellite s orbital speed. In this case you add the distance from the center of the earth to the surface of the earth 6 38 10 6 meters to the satellite. M s b find the period of its revolution. Because the radius and period are related you can use physics to calculate one if you know the other.

It is the same thing as 6 371 000 meters. A 796 kg satellite is in a circular orbit about the earth at a height above the earth equal to the earth s mean radius. The earth s mass is 5 98 x 10 24 kg and it radius is 6 38 x 10 6 m. When a satellite travels in a geosynchronous orbit around the earth it needs to travel at a certain orbiting radius and period to maintain this orbit.

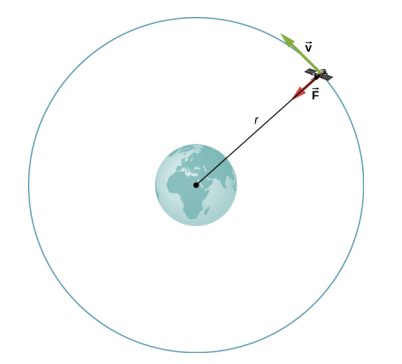
Units h c find the gravitational force acting on it. Or you could even write this as 6 371. The distance between the center of mass of earth and the center of mass of this object which is sitting at the surface of the earth. And we re going to square this.

That s the radius of the earth. The radius of the earth is 6 4 x10 6m and g 6 67 x 10 11 n m 2 kg 2 a.